the post where the internet corrected me and I learned something

edit: I wrote this, it shall remain as written--but check out the comments because it's a good example of strangers on the internet being informative and helpful! Special thanks to The Happy Anarchist, Olav M., and Robert C.: you three rock! Ray, I'm sorry I doubted you.

I wrote a post a while back about this. Unknown in the comments didn't seem to get how bell curves work, or didn't think they applied, and I tried to remedy that.....and then, after a few exchanges, I thought "wait, am I trying to convince someone on the internet??" and (with as much good humor as I could muster) I decided to let Unknown's ignorance continue unopposed.

But then I stumbled through to this other post, where the author (why, Ray, why!?) seems to be asserting the same thing as Anon: that d66 is a flat, curve-less probability like any single-die roll.

And now I'm thinking "am I the ignorant one?!?".... so, here's me presenting my thinking. (Although my personal thinking shouldn't have anything to do with it, because probability operates whether or not I believe in, or understand, it)

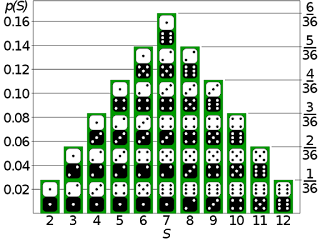
This reference taken from HERE

I'll start with doubles, because that seems the clearest example for the "d66 isn't 2d6" crowd.

Say I roll my first die. There is a 1 in 6 chance of any number coming up, which is a flat distribution. Let's say I roll a 4.

Now, for my second die there is a 1 in 6 chance of another 4 coming up (44-Questing Knight, yeah!). There is a 5 in 6 chance that a number other than 4 will come up, that I will not roll doubles. These are not equal probabilities. which means that all results are not equally likely. Or, to parse it another way: if doubles are less likely than the other results, than all results are not equally likely.

It may be tempting to treat each roll as equal (for those of you pointing and saying "it's a 1 in 6 chance of a four each time!"), but that is only the case if they are unrelated rolls. As soon as we decide "this roll and this other roll are combined to get the result" they are related, with the second roll building on the specificity which the first roll provided. 

We can call it d66 forever, but we shouldn't fool ourselves into thinking that we are rolling something other than 2d6. And 2d6 conforms to a bell curve, which is a measure of probability in aggregate, not a measurement of individual rolls. Individual rolls may seem to land anywhere on the curve with equal likelihood, yet 500 aggregated rolls will clearly show the effect of the curve.

Check out that image above closely: it shows how the d66 results are grouped in terms of likelihood. If you think the math in the image is wrong try grabbing 2d6, and rolling for Backgrounds 50 times, marking down the result each time. How many Ardent Giants did you roll? How many Zoanthrops? How many Backgrounds that add up to 7 (Claviger, Fellowship of Knidos, Lonesome Monarch, Poorly-made Dwarf, Academy of Doors, Thinking Engine) did you roll?

Anecdotally (though anecdotes shouldn't matter as much, because probability occurs without regard for my personal experience), out of the dozen or so players I've had pass through my Troika! game there have been three Poorly Made Dwarfs, two Vengeful Children, and Two Exotic Warriors rolled. There were some other repeats(Claviger, Thinking Engine), which I let the players reroll.

Hopefully this clarifies things. That, or someone more math-knowledgeable than I can explain in the comments how my understanding of this is wrong.